

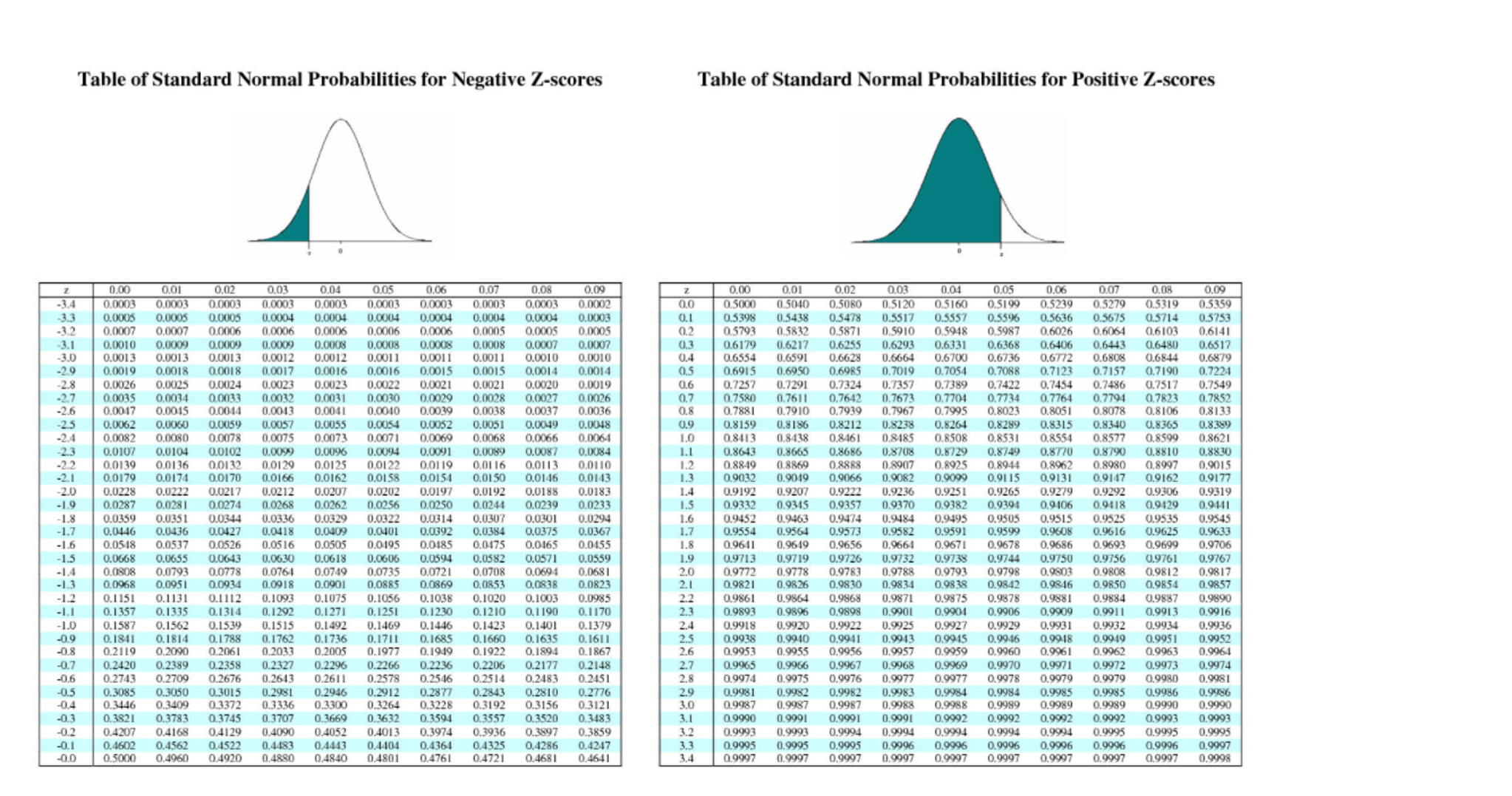
You can think of a z-score as the number of standard deviations there are between a given value and the mean of the set. Z-scores are related to the Empirical Rule from the standpoint of being a method of evaluating how extreme a particular value is in a given set. It is worth noting, particularly for US students, that the instructor uses the notation x rather than µ for mean, and pronounces z as “zed.” Many non-parametric test statistics, such as U statistics, are approximately normal for large enough sample sizes, and hence are often performed as Z-tests.The British video below is very clear and easy to follow. Z-tests are employed whenever it can be argued that a test statistic follows a normal distribution under the null hypothesis of interest. Although there is no simple, universal rule stating how large the sample size must be to use a Z-test, simulation can give a good idea as to whether a Z-test is appropriate in a given situation. When using a Z-test for maximum likelihood estimates, it is important to be aware that the normal approximation may be poor if the sample size is not sufficiently large. If the population variance is unknown (and therefore has to be estimated from the sample itself) and the sample size is not large ( n μ 0, it is upper/right-tailed (one tailed).įor Null hypothesis H 0: μ=μ 0 vs alternative hypothesis H 1: μ≠μ 0, it is two-tailed. Therefore, many statistical tests can be conveniently performed as approximate Z-tests if the sample size is large or the population variance is known.
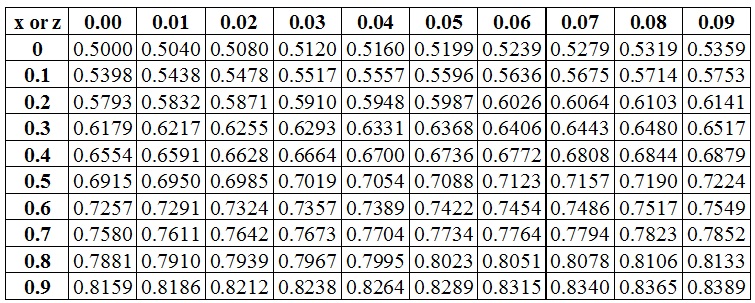
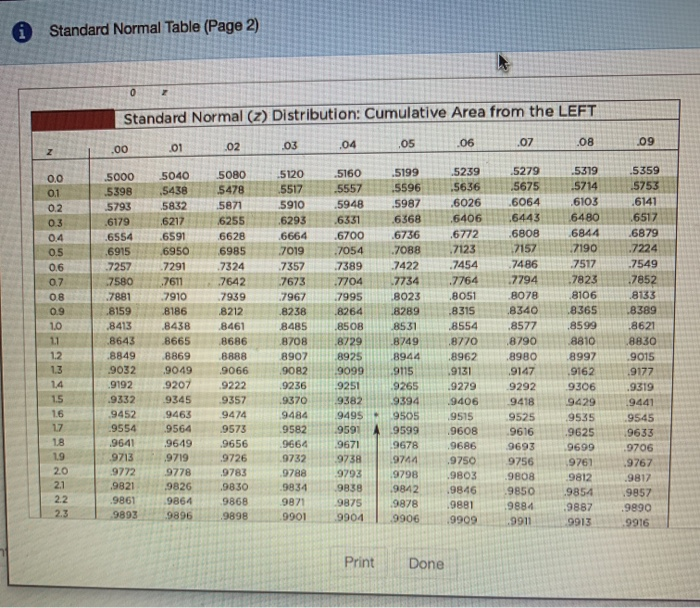
However, the z-test is rarely used in practice because the population deviation is difficult to determine.īecause of the central limit theorem, many test statistics are approximately normally distributed for large samples. Both the Z-test and Student's t-test have similarities in that they both help determine the significance of a set of data. For each significance level in the confidence interval, the Z-test has a single critical value (for example, 1.96 for 5% two tailed) which makes it more convenient than the Student's t-test whose critical values are defined by the sample size (through the corresponding degrees of freedom). For the "Z-test" procedure in the graphics pipeline, see Z-buffering.Ī Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution.


 0 kommentar(er)
0 kommentar(er)
